Understanding Big O Notation

Big O is a highly popular notation that is often heard in the world of algorithms, performance and optimization. It is a pivotal topic for coding interviews at big companies such as Google, Amazon, Facebook... everybody says you should learn about it, but why? why would you or anyone learn about Big O if you are not taking interviews? In this article, I will try to explain from my perspective what Big O is, why it is useful and how you can apply it in an everyday basis to make you improve as a software developer.

Definition

There are multiple ways of writing algorithms, you can implement a feature using different approaches, everybody has a unique way of thinking and solving their way through problems, for this reason, we need a way to understand how these different solutions perform under different scenarios to help us determine which one works better based on our needs, Big O is a notation that allows us to evaluate this, specifically it allows us to evaluate growth rates by analyzing how time complexity (Time of execution) and space complexity (memory usage) scale for a given algorithm when larger input sizes are processed by it. Big O is driven by the upper bound or higher complexity found in an algorithm so the worst case complexity will be the Big O representation of your code..

For a formal definition of Big O I would recommend you to read the one from wikipedia which is pretty straightforward, if you have trouble understanding the formal definition do not worry, it is enough to understand the intuitive definition highlighted above.

Understanding How to Evaluate Complexities

To understand how to evaluate an algorithm or a piece of code we need to separate it into statements or operations and we need to understand how each of these affects the algorithm.

Let's define some important concepts before proceeding:

1. Complexity and Performance are two different things, The former specifies how the required resources for a program scale and the latter specifies how much of those resources are used taking into consideration the environment (the machine) in which an algorithm is running, the code, the time... So Complexity affects Performance but this is unidirectional, performance does not affect complexity.

2. Statements are the units or simple instructions executed in a program to perform an action, they could be in example:

   • Defining a variable let a = 1;
   • Making an arithmetic operation 3 + 2
   • A Function call fn()

There are also Compound Statements that contain more than one instruction or operation, one example is: for (let i = 0; i < 10; i++) {} which is executing a loop but at the same time defining a variable i, making a comparison i < 10 and incrementing the variable i by 1 in each iteration.

The idea is that you understand that programs are a set of statements that determine their complexity. In Big O specifically, we care about the statements with higher complexity, where "higher" means less efficient, so after evaluating all the statements the one that will define the complexity of the algorithm is the less efficient complexity found, so:

Big O = max(complexity(statement1), ..., complexity(statementN))

Finally, two more concepts, as previously mentioned there are two types of complexities relevant to Big O:

3. Time Complexity evaluates how an algorithm will scale over time, helping us understand if it will be too slow or will be fast enough for our needs.
4. Space Complexity evaluates how an algorithm makes use of space over its execution, for example, how many variables we are defining, how an array or object grows to ensure that we will not cause any issues with memory consumption given our needs...

Constant

Constant or $O(1)$ Complexity refers to an algorithm that no matter the input size it will always take the same amount of time/space to perform a task (therefore it is constant when the input size grows), in example let's evaluate a function that validates if the first element of an array is a number:

function isFirstElementNumeric(list) {
    return typeof list[0] === 'number';
}

If we evaluate this by statements we understand that:

• Line 1: We are creating a function called isFirstElementNumeric
• Line 1: We are creating a variable called list to hold the input.
• Line 2: We are returning a value
• Line 2: We are getting the typeof list[0]
• Line 2: We are making a comparison against number

Notice how I have separated the lines into multiple statements, one line can have multiple statements, and some of those statements can be native implementations of the language like in this case when typeof is used, and this is important to understand, the inner implementation of native functionalities affects the complexity of an algorithm depending on how it is implemented by the language, so if you are evaluating an algorithm, you need to be careful to understand and account for the complexity of the inner works of the language.

If we evaluate the Time Complexity of the previous algorithm knowing the concept of constant we can determine that each statement is $O(1)$, why? because for all the statements of this function no matter how big the input is, it will always take the same amount of time to evaluate every statement of the function, because in this case even if the array has 1000 elements we are just taking index 0 and same goes for space, we are not defining new variables when executing this function, and this next part is important, yes, we are using a variable list to hold the input but when evaluating space complexity we don't take into consideration the input itself because that is the very premise upon which the algorithm evaluation itself is based on, if we considered the input, then, for any function receiving a data structure capable of storing multiple properties it would be at least linear time (We will explain linear time in a bit).

The graph below represents how time complexity (Y Axis) gets affected when the input size (X Axis) grows, since time is constant time remains unchanged for any given input size.

Real-life usage of constant complexity

Pretty much everywhere, i.e:

• Arithmetic operations
• Variable definitions
• Boolean Comparisons

Logarithmic

Also known as $O(log(n))$, As the name specifies, we determine a logarithmic time complexity when an algorithm runs in a time that is proportional to the logarithm of the input size as its size grows.

Logarithms can have different basis, so for example for a log of base 10:

1. log(1) = 0
2. log(2) = ~0.301
3. log(3) = ~0.477

and so on... As you can see the growth rate is still small and not linear. Usually, we are able to identify an algorithm that is $O(log(n))$ because it will divide itself into smaller and smaller pieces with each iteration or operation, the simplest example I can think of is the following:

function showIteratedValues(n) {
    let i = 1;
    let list = [];

    while (i < n) {
        i = i * 2;
        list.push(i);
    }

    return list;
}

If we evaluate this statement by statement we realize that lines 1,2 and 3 are constant time and in space, because we are defining a function and some variables and they do not change in respect of the input n, but when we reach the while statement things get interesting.

The while statement creates a loop based on the condition i < n, so the cycle will execute until that condition is false, this already takes more than constant time to execute, why? because for a bigger input n passed to this function the algorithm will take a longer time to execute because the while loop will have to potentially execute more iterations. With each iteration, the value of i will exponentially increase because we are multiplying i by 2 and in the next iteration the result * 2 and so on (you might be thinking "wait, exponentially?, aren't we talking about logarithmic time here?") yes, this is true but something important to notice is that logarithmic growth is the inverse of exponential growth meaning that if the loop's variable condition is increasing exponentially then the number of executions needed by the loop to finish decreases logarithmically, hence the time complexity is logarithmic.

How about space complexity? Good question, let's evaluate the statements in the loop:

1. i = i * 2; for the definition of the variable i inside of the while loop we can say that the space complexity is constant, why? because with each iteration the value of i is overwritten with the new value of i * 2, so this is not growing in space.
2. list.push(i) this right here is the key to the space complexity of this algorithm, every time an iteration happens the array list grows in parallel with time complexity, hence the space complexity of this statement is logarithmic.

And so the space complexity of this complete algorithm is logarithmic.

Real-life usage of logarithmic complexity

• Binary Search.

Linear

One of the easiest complexities to identify along with constant, an algorithm has a linear $O(n)$ complexity when it grows proportionally to the input, in other words when the growth rate is fixed when iterating over each input given:

function elevateToPowerOfTwo(list) {
    const n = 100;
    const powerOfTwoList = [];

    for (let i = 0; i < n; i++) {
        powerOfTwoList.push(i**2);
    }
}

Let's evaluate by statements again:

1. The first three lines of code are constant time and space, they are not changing for a bigger input.

2. for the for loop we have for (let i = 0; i < n; i++) { which contains 4 statements:

   • let i = 0; which will get overwritten next time when it is incremented so it is constant.
   • i < n a simple comparison constant.
   • i++ increments i by 1 on each iteration, the value of i changes but the variable i is overwritten.
   • The for statement itself, we will need to iterate over each value until i < n is no longer true, if n is a higher value we will have to iterate as many times as needed again until i reaches a value >= n and this is true of any n for this algorithm, as you can notice in linear time the correlation of the input size with the runtime is clear, if we increase n by a factor of 2 we already know that we will have to iterate twice as many times as before.

For Space complexity we can proceed to evaluate the next statement:

3. powerOfTwoList.push(i**2); which increases the array with each iteration until the loop is over, since the loop itself is linear time this array will grow in space at the same rate hence space complexity is linear.

if we compare this with logarithmic time complexity we will notice that logarithmic time is a bit more ambiguous, nevertheless, it is worth noting that logarithmic time is more efficient than linear because logarithmic time grows at a slower rate (due to the partitioning that happens through each iteration, thing that does not happen in linear time).

Real-life usage of Linear complexity

• loops
• Recursive Functions

Linearithmic

Linearithmic complexity is a combination of linear and logarithmic complexity hence $O(n \times log(n))$

Linearithmic algorithms are slower than $O(n)$ algorithms but still better than quadratic time algorithms (which we will see in a bit) a way to see them iteratively speaking is by combining our linear and logarithmic code examples, to end up with a linear cycle executing a logarithmic one inside so that:

But this is just one way to express it in code, linearithmic algorithms have many ways of presenting themselves recursively and by input division over time...

Following the iterative idea from before we could write:

function logarithmicExecutions(n) {
    for(let i = 0; i < n; i++) {
        let j = 1;
        let counter = 0;
        let logarithmicPossibilities = [];

        while (j < n) {
            j = j * 2;
            counter++;
        }

        logarithmicPossibilities.push(counter)
    }
}

Evaluating the code above and already having evaluated linear and logarithmic time complexity it becomes even clearer why it is linearithmic, however, the space complexity of this piece of code is not linearithmic, if you take a look closely it is linear space complexity given that logarithmicPossibilities grows proportionally to the outer loop which is $o(n)$ and the rest of the variables are overwritten per iteration.

Real-life usage of Linearithmic complexity

they are usually found in sorting algorithms such:

• Merge Sort
• Heap Sort

Quadratic

An algorithm ison quadratic time or space complexity $O(n^2)$ when it grows proportionally to the squared value of the input given so:

• For $1$ we define $1^2 = 1$
• For $2$ we define $2^2 = 4$
• For $3$ we define $3^2 = 9$

and so on... visually speaking quadratic time would look something like this:

a good example of this type is when we are dealing with nested loops (one level of nesting), it does not mean that all nested loops are quadratic by any means, and I will explain this better below, but a typical case could be the next one.

const list = [1,2,3];
let total = 0;

for (let i = 0; i < list.length; i++) {    total += i;    for (let j = 0; j < list.length; j++){        total += j;    }}
console.log(total);

If you take a look at the code above you'll see that we have an outer loop that executes up to $n$ times where $n = 3$ (the length of list), inside of that loop we have another one that is doing the same thing, which means that for each element on the parent loop we are executing $n$ times the inner loop:

So basically $n \times n$ hence $n^2$, however not all nested loops represent a quadratic time complexity, this only happens in cases where the two loops (outer and nested loop) are running the same amount of $n$ times, in the code example above using list.length as $n$, but what happens if one of the loops has a different variable with a different size? - well in that case the complexity would be $O(n \times m)$, because both variables are distinct.

As for the space complexity of our algorithm above it is constant $O(1)$ because memory is not increasing concering the input.

Real-life usage of quadratic complexity

• Nested loops
• Bubble Sort

Exponential

Also known as $O(a^n)$ where $a$ is constant and $n$ is variable, not to be confused with polynomial where it is the opposite.

A simple example I can think of that takes exponential time is recursive Fibonacci without memoization (If you don't know what memoization is take a look at one of my previous articles Avoid recomputing heavy tasks by leveraging memoization in javascript).

let's take a look at the code:

function fibonacci(num) {
    if (num <= 1) {
        return 1;
    }

    return fibonacci(num - 1) + fibonacci(num - 2);}

so why is it exponential? I think it is useful to look at a visualization to understand what is happening here:

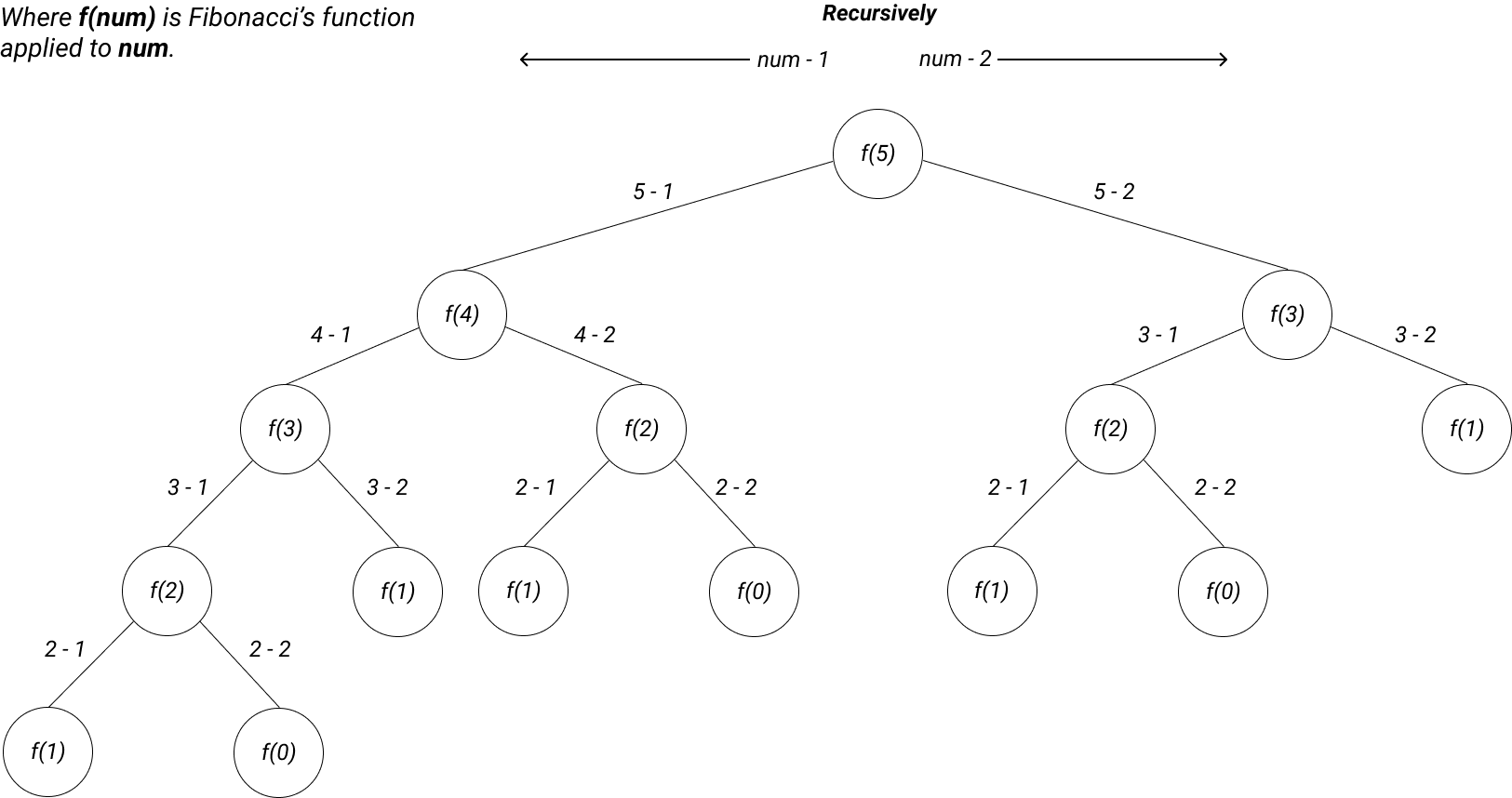
For each new function call, the algorithm doubles the previous amount of executions which tells us that the exponent $n$ is increasing with each recursive call in this case for base 2.

Note: There is a theorem that helps us determine the complexity of recursive algorithms called Master Theorem but it deserves its own article.

Real-life usage of Exponential complexity

• Exponential algorithms in the form of $O(a^n)$ which usually solve a problem of size $n$ by recursively solving $a$ smaller problems of size $n-1$.
• Fibonacci sequence.

Factorial

Factorial time $O(n!)$ is not an indicator of good performance but sometimes we can't do better than that, to put you into context let's remember its definition: The factorial of a non-negative integer number $n$ is the product of all positive integers less than or equal to $n$.

Factorial algorithms are often found when making permutations and combinations.

so for example, the factorial of 4:

Real-life usage of Factorial complexity

A classic case scenario of this time complexity is the processing of every possible permutation of an array where $n$ is the size of the array and so it is $n!$ because we need to make all the permutations possible up to the length of $n$.

• Permutations
• Combinations

Due to complexity I have decided that I will write a separated article to explain one example of factorial complexity.

Hierarchy

So after everything we have learned, we can define that for an $n$ large enough it holds that:

$O(1) < O(log(n)) < O(n) < O(n \times log(n)) < O(n^2) < O(2^n) < O(n!)$

Which means that if you are evaluating your code and you find that it has an statement that is $O(n)$ but there is another block of code that is $O(n^2)$ then your code is $O(n^2)$ because as previously mentioned, Big O cares about the upper bound.

There are other complexities that we are not including in this article like in example cubic complexity, but the idea is not to name them all, instead, I want to help you understand how to analyze your code to determine how efficient it is and of course dig deeper into the topic if you are interested.

Apply this knowledge in your day to day basis

One way to start practicing Big O notation is by thinking on the complexity of the problems you are solving, go back to problems you have previously solved, and see for fun if you can determine their complexity and if there is room for improvement for a future state, this is a very useful practice that will help you practice statement's complexity evaluation so that it becomes easier and easier, however, this does not mean that you need to refactor all your code, NO!, before doing improvements, make sure to measure if it is a real problem given the use case of the algorithm, don't apply blind micro-optimizations since that is not a good practice either, I have written an article on that matter called Code quality and web performance, the myths, the do's and the don'ts in case you wanna check it out.

When making a new implementation think in terms of scalability, feel free to do a naive implementation first and apply gradual improvements from there or take your time thinking on the implementation to get it right the first time, either way works, the important part is to think in terms of how each statement you are adding affects the algorithm as a whole.

Code reviews are also a perfect place to put this into practice, understand the business application of the code that you are reviewing but also the complexity that is being added to the codebase and see if it can be improved and if it is worth it.

Closing Thoughts

I have to say, writing this article was a lot of fun, I hope that I was able to incentivize you to keep learning about algorithms and their complexities, this is just a little part of everything that involves algorithm's complexities, in example besides Big O (O) we also have Big Omega ($\Omega$) to evaluate the lower bound, and Big Theta ($\Theta$) to evaluate the average case, so please do not stop here, if you have any comments or wanna reach out feel free to do it, as always the information is below.

See you next time!